STEP #05 - Il principio fisico



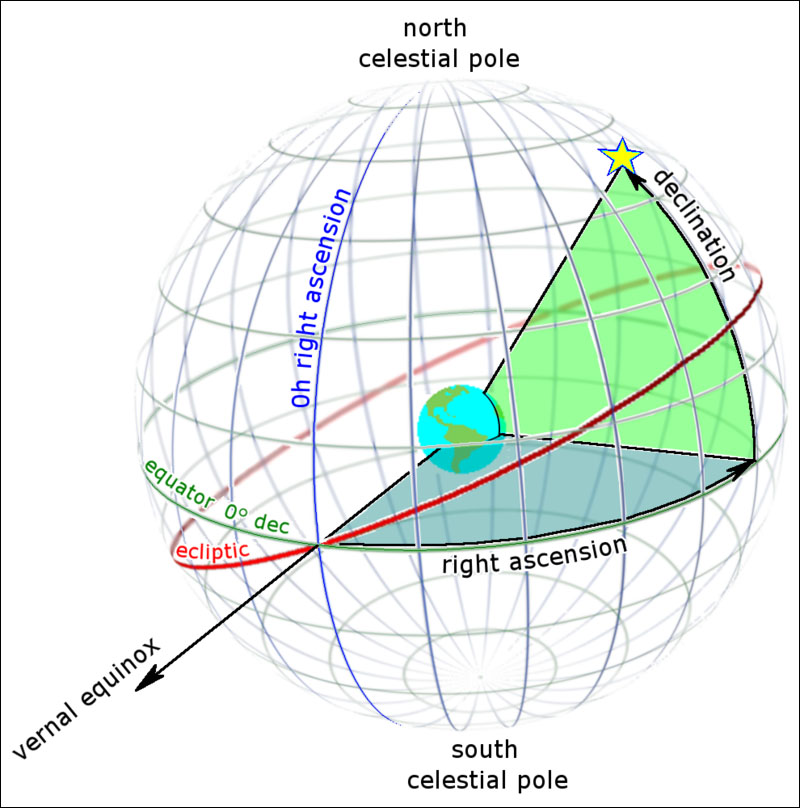
Lo strumento dei passaggi permette di misurare la posizione delle stelle in transito attraverso un meridiano sfruttando il sistema di coordinate equatoriali, consistente in ascensione retta (α) e declinazione (δ). Queste ultime non sono altro che l'equivalente astronomico rispettivamente di longitudine e latitudine.

Dato che le stelle si muovono sulla volta celeste in maniera simile al Sole, esse raggiungono il punto più alto quando passano sul meridiano e, dato che la Terra ruota a velocità angolare costante, lo fanno sempre nello stesso istante di tempo (siderale) ogni giorno.

Una volta che lo strumento dei passaggi viene allineato al meridiano, l'ascensione retta può essere determinata conoscendo il tempo siderale locale (TSL), dato che vi corrisponde:

\[ \alpha = \text{TSL} \]

La declinazione viene calcolata tramite la distanza della stella osservata dallo Zenit (ZD), secondo la seguente formula

\[ \delta = L \pm ZD \]

dove $L$ è la latitudine dell'osservatore, a cui la distanza dallo zenit viene aggiunta o sottratta a seconda che la stella osservata si trovi a nord o a sud dello zenit.

Fonti:

http://www.thegreenwichmeridian.org/tgm/articles.php?article=6

https://www.physics.ncsu.edu/classes/astron/Right_Ascension.html

https://cseligman.com/laboratory/navcalc.htm

https://skyandtelescope.org/astronomy-resources/right-ascension-declination-celestial-coordinates/

Commenti

Posta un commento

Post popolari in questo blog

STEP #27 - La mappa concettuale

Immagine
Di seguito è riportata una mappa concettuale che rappresenta gli aspetti principali dello strumento dei passaggi. Ovviamente viene riportato lo sviluppo della scienza astronomica tramite l'osservazione celeste con una corrispondenza bidirezionale e vengono poi indicati due campi strettamente legati all'astronomia, ovvero la navigazione e la misurazione del tempo.  La navigazione e l'astronomia sono strettamente correlati, visto che la posizione delle stelle è sempre stata usata per orientarsi in mare. Lo strumento dei passaggi è stato infatti largamente utilizzato nel XIX secolo per compilare gli almanacchi nautici . La misurazione del tempo è un altro concetto strettamente legato all'astronomia perché la misura del tempo, prima dell'invenzione dell' orologio atomico , era affidata alla regolarità del movimento apparente del Sole nella volta celeste. La misura del tempo, inoltre, si collega a un altro concetto fondamentale, ovvero la precisione. Allo strumento d
Continua a leggere

STEP #28 - La sintesi finale

Arrivati alla fine di questo percorso risulta necessario offrire una visione di insieme del lavoro fatto. Si è iniziato con informazioni di carattere generale sullo strumento dei passaggi, quali la definizione e la sua denominazione in varie lingue ( STEP #01 ), nonché un'immagine che ne ritrae uno risalente al XIX secolo ( STEP #02 ) e un glossario ( STEP #03 ) che raccoglie tutti i termini relativi allo strumento in esame. Post successivi di carattere generale e informativo sono stati quello relativo alla tassonomia ( STEP #14 ), in cui lo strumento è stato classificato all'interno di un albero riguardante la famiglia dei telescopi, lo step sulle anatomie ( STEP #16 ), l'abbecedario ( STEP #19 ), in cui tramite un piccolo esercizio è stata realizzata una lista di parole chiave utili nella descrizione dello strumento, e quelli sui numeri ( STEP #15 ) e sul simbolo ( STEP #06 ), finalizzati a riportare una rappresentazione più immediata dello strumento. Sono state fornite a
Continua a leggere